Exercises

Multiple Regression and Beyond (3e) by Timothy Z. Keith

library(tidyverse)
library(lavaan)
library(semTools)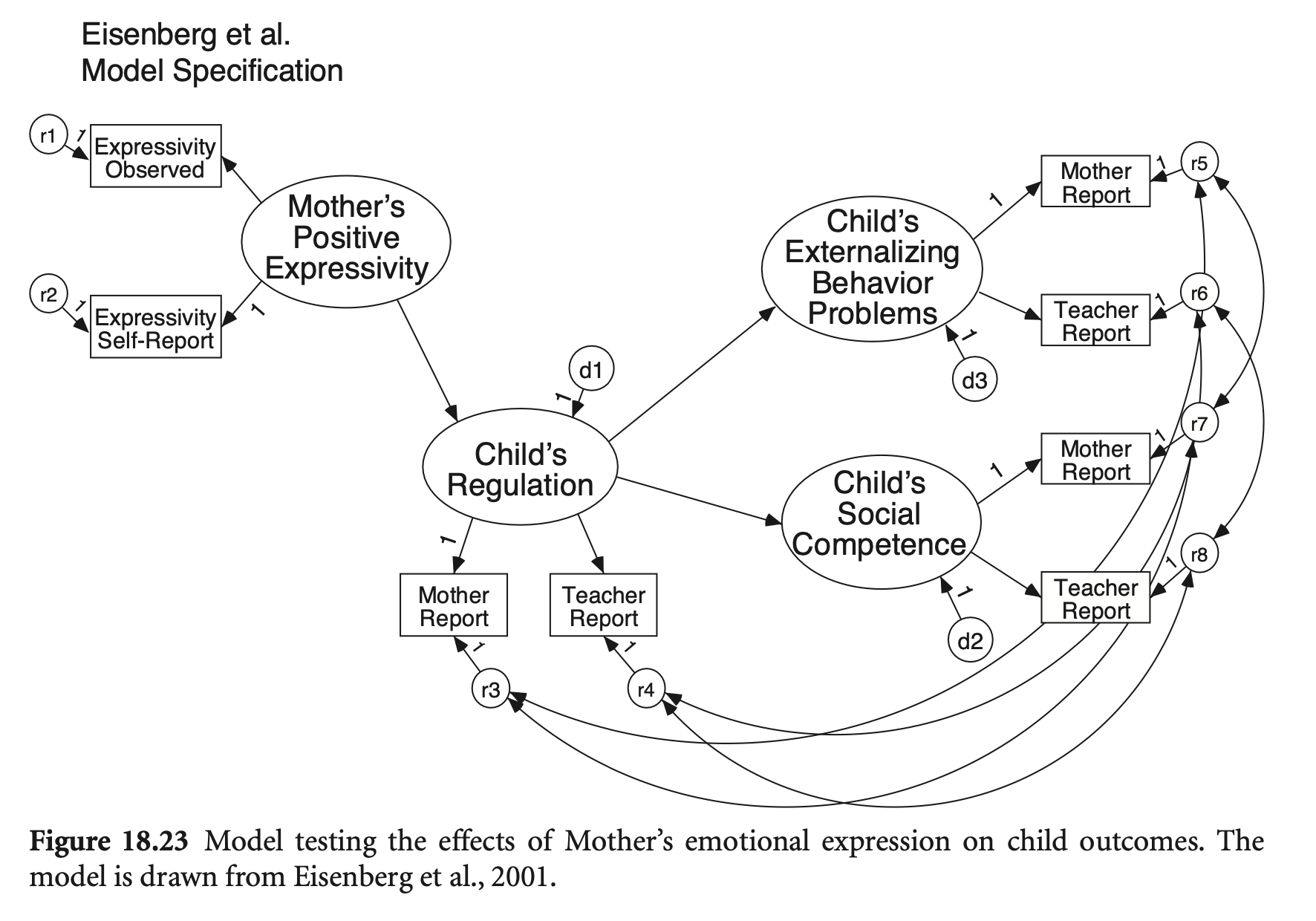

18장 잠재변수모형 II 연습문제 2번. (1) ~ (4)

Residual covariance에 대한 제약

• 교사 보고(teacher report)로 측정된 변수들 간의 상관을 모두 추정; 3개
• 어머니 보고(mother report)로 측정된 변수들 간의 상관을 모두 추정; 3개
• 두 개의 최종 변수들(행동문제 외현화, 사교역량)은 서로 독립; 1개

# load data
eisenberg <- haven::read_sav("data/chap 18 latent var SEM 2/Eisenberg et al 2001.sav") |> 
  rename(ext_mr = exter_mr)

eisenberg |> print()

# A tibble: 176 × 8
  exp_mo exp_msr reg_mr   reg_tr ext_mr ext_tr   soc_mr soc_tr
   <dbl>   <dbl>  <dbl>    <dbl>  <dbl>  <dbl>    <dbl>  <dbl>
1 -1.70        6 -0.257 -0.474       29      9  0.350    0.402
2  2.19       10  1.49   1.51         1      4  0.509    0.706
3  0.959       6 -0.628 -1.50        27     22  0.00530 -1.71 
4  0.925       7  1.24  -0.00363     23     15  1.49    -0.825
5  1.66        6 -0.567  0.455       17     14 -0.386    0.299
6  1.62        7 -1.80  -0.530       24     15 -1.60    -0.128
# ℹ 170 more rows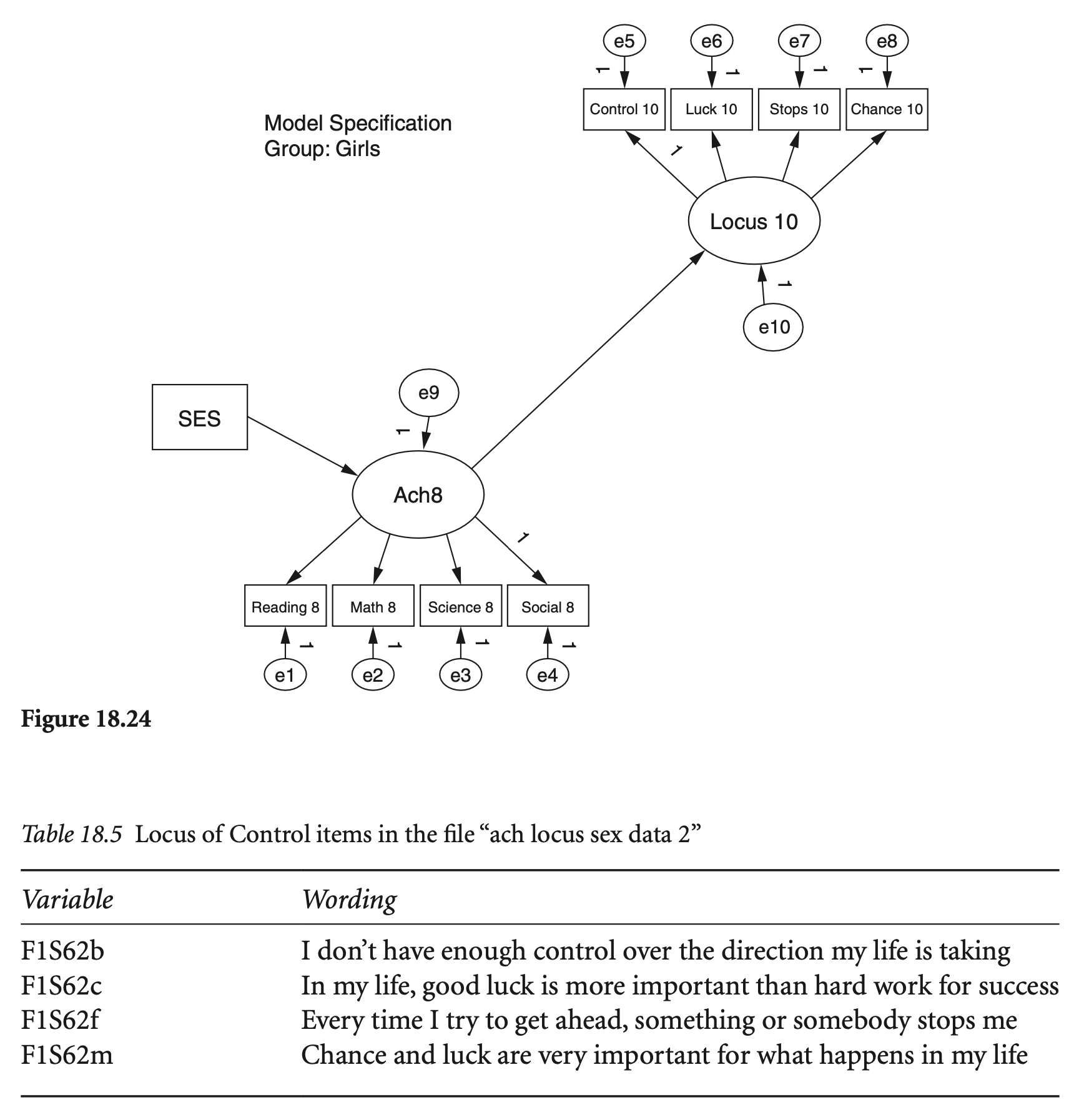

18장 잠재변수모형 II 연습문제 4번.

# load data
nels <- haven::read_sav("data/chap 18 latent var SEM 2/ach locus sex data 2.sav")
nels |> print()

# A tibble: 857 × 10
  byses     sex        bytxrstd bytxmstd bytxsstd bytxhstd f1s62b  f1s62c  f1s62f  f1s62m 
  <dbl+lbl> <dbl+lbl>  <dbl+lb> <dbl+lb> <dbl+lb> <dbl+lb> <dbl+l> <dbl+l> <dbl+l> <dbl+l>
1 -0.563    2 [Female] 65.5     59.5     64.7     67.8     3 [DIS… 3 [DIS… 3 [DIS… 2 [AGR…
2  0.123    1 [Male]   50.6     48.0     49.1     46.9     2 [AGR… 3 [DIS… 2 [AGR… 2 [AGR…
3  0.229    2 [Female] 59.1     42.8     49.1     47.9     2 [AGR… 2 [AGR… 3 [DIS… 2 [AGR…
4  0.687    1 [Male]   44.4     49.2     35.5     57.3     3 [DIS… 3 [DIS… 3 [DIS… 3 [DIS…
5  0.633    2 [Female] 63.3     52.5     51.8     52.1     2 [AGR… 3 [DIS… 2 [AGR… 3 [DIS…
6  0.992    1 [Male]   31.8     44.5     39.5     38.3     3 [DIS… 3 [DIS… 3 [DIS… 3 [DIS…
# ℹ 851 more rows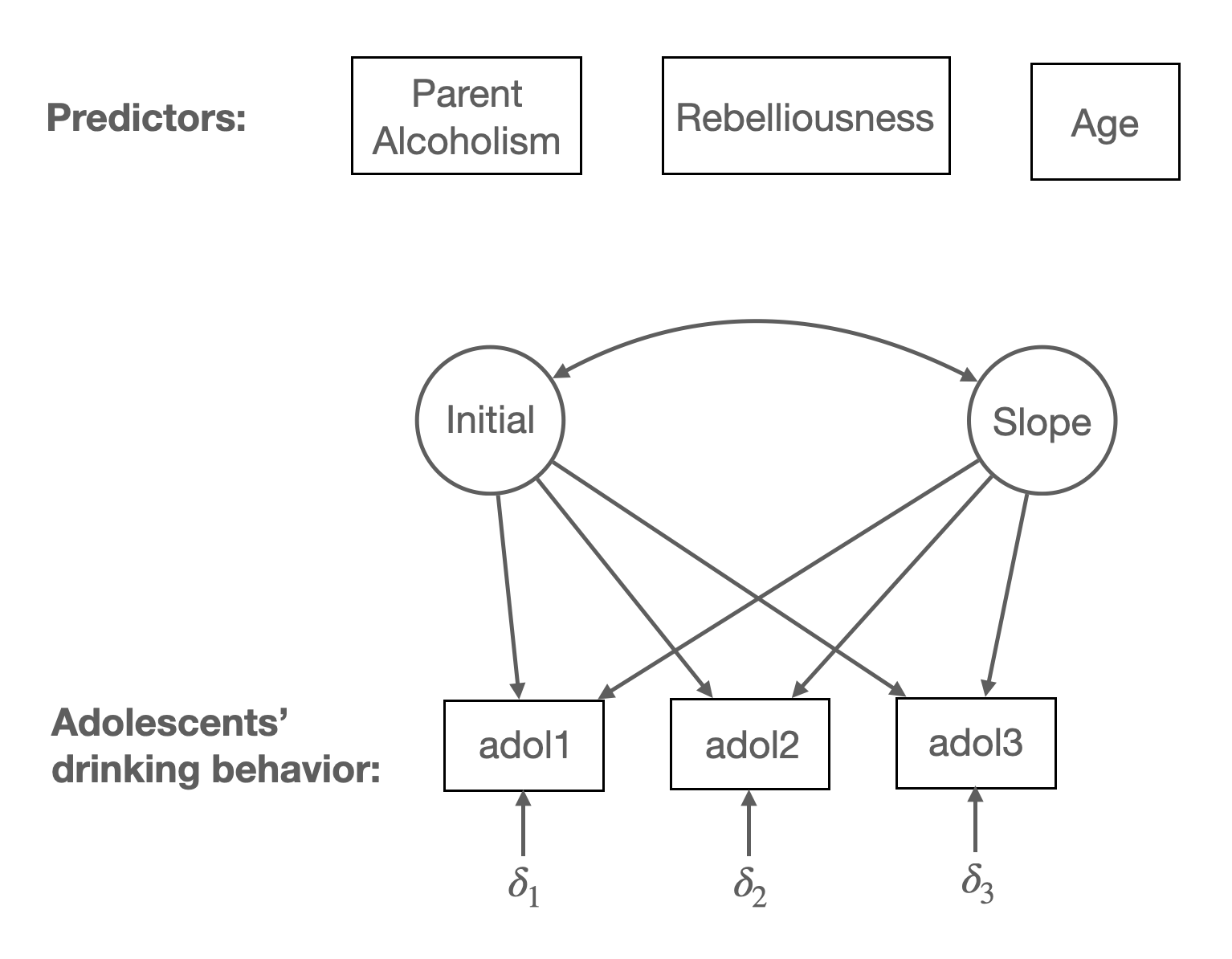

21장 잠재성장모형 연습문제 2번. (1) ~ (4)

# load data
vars <- c("adol1", "adol2", "adol3", "rebel1", "age", "sex", "parent")
sd <- c(2.81, 3.98, 4.79, 0.69, 1.4, 0.5, 0.49)
lower <- "
1
0.68 1
0.5 0.68 1
0.3 0.29 0.32 1
0.31 0.31 0.23 0.14 1
0.01 0.06 0.1 0.14 -0.03 1
0.12 0.17 0.2 0.12 -0.15 0 1
"
alcohol <- getCov(lower, names = vars, sd = sd)
mean <- c(1.36, 2.12, 3.18, 2.58, 12.91, 0.52, 0.56)

데이터가 아닌 공분산과 평균으로 추정하니, 다음과 같이 모형을 추정할 때, 표본의 공분산 행렬, 평균값, 표본 수를 이용해 진행하세요.

growth(model, sample.cov = alcohol, sample.mean = mean, sample.nobs = 363)